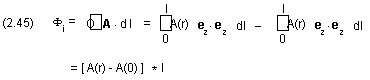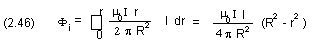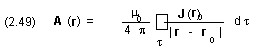A Formulation of the Problem

1. Summary:

A method of calculating the eddy currents in conductors of uniform cross-section excited by a current source applied continously to a conductor is presented. It is shown that the analysis of eddy currents in conductors leads to a partial differential equation (the diffusion equation consisting of the magnetic vector potential A and the source current density vector Js which in general is a function not only of the space variables but also a function of the temperature T) and one constraint equation. The non-homogenous diffusion equation for the magnetic vector potential changes to Laplace's equation in the surrounding medium. An approximation solution based on the finite difference and finite element method is presented for the case of a single conductor having a circular cross section which is important in physics and electrical engineering. The application of the methods is illustrated by this example and compared with the analytical result available in this case.

1. Maxwell's Equations in Differential Form

The governing equations for the time varying field problems are given by Maxwell's equation: [2.1, 2.2]

(2.1) curl H = J + ∂D/∂t (Ampere's Law)

(2.2) curl E = - ∂B/∂t (Faraday's Law)

(2.3) div D = r (Gauss' Law)

(2.4) div B = 0 (no magnetic sources)

where

H ... magnetic field intensity vector

J ... current density vector

D ... electric displacement (electric flux density) vector

E ... electric field intensity vector

B ... magnetic induction (flux density) vector

r ... volume charge density.

Maxwell's equations specify the relations among the four field vectors E, B, D, and H, and between the charge density, r, and current density, J.

For further development of the the theory it will be necessary to reduce the number of field vectors by imposing conditions on the electromagnetic properties of the medium. These conditions are called constitutive equations and involve constants which are characteristic of the medium. While in general the constitutive equations need not be simple, we shall restrict ourselves to media which have linear properties, and which are, furthermore isotropic and homogeneous.

The constitutive equations assumed are

(2.5) D = e E

and

(2.6) n B = H

where

e ... is the permitivity (dielectric constant) of the medium

n ... is the magnetic reluctivity of the medium

We shall assume the relationship between J and E:

(2.7) J = s E

where

s ... is the electrical conductivity of the medium.

This relation is known as the elementary form of Ohm's law. Finally, the permeability, m, is 1/n.

The above parameters e, n, and s are assumed to be constants, unless otherwise stated. It should be stressed that the material constants are in general field, frequency and temperature dependent.

The direct determination of E and B by solving Maxwell's equations is usually difficult. The solution is often facilitated by defining potential functions in terms of the field vectors, because it is possible to transform the four first-order field equations to second-order equations in the potential functions that are formally integrable, if the boundary conditions are given. From the potential functions, it is possible to calculate E and B and the distributions of current densities and charge. Frequently, the current densities and charge are more conveniently determined directly from the potential functions than from the field vectors.

To achieve this aim, we first note that the solution for the magnetic induction B must satisfy equation (2.4), i.e. its divergence must vanish everywhere. Since the divergence of the curl of any vector vanishes identically, the equation is satisfied automatically if B is expressed as the curl of a vector:

(2.8) B = curl A = — x A

where

A ... is the magnetic vector potential

However, the vector function A is only determined by equation (2.8) for a given magnetic induction B to within an arbitrary vector constant.

To define a scalar potential it is necessary to find a vector with a vanishing curl. From the symmetry of electric and magnetic field quantities, the second field equation (2.2) should be used for this purpose, since this is the electric analogue of the Maxwell's fourth equation (2.4).

Expressing B in equation (2.2) in terms of the vector potential A, we obtain

(2.9a) curl E = - ∂(curl A)/∂t

or

(2.9b) curl (E + ∂A/∂t) = 0.

The vector (E + ∂A/∂t) is a potential vector because its curl vanishes. It can be derived from the electric scalar potential function f defined by

(2.10) - grad f = E + ∂A/∂t

where f is any differentiable field and satisfies Laplace's equation. Equations (2.8) and (2.10) leave much latitude in the choice of A and f , but certain restrictions come into play when the inhomogeneous or source equations are introduced.

The geometric representation of equation (2.10) is shown in Figure 2.1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Fig. 2.1 The electric field intensity is the vector sum of -—f

and -∂A/∂t.

 

The scalar potential defined by equation (2.10) is called the electric scalar potential.

To obtain the differential equations for the vector and scalar potentials we shall confine ourselves to a linear, isotropic, and homogenous medium. Then, the number of independent field vectors may be reduced by two through the constitutive equations. Let the medium have permitivity e and reluctivity n, and write the remaining Maxwell's equations as

(2.11) curl curl A = J + ∂E/∂t

and

(2.12) div E = r / e .

Now eliminate E and B from the field equations. The scalar f is defined to within an additive constant by (2.10), but the vector A is not defined completely by (2.8). To define a field vector, both its curl and divergence must be specified. No conditions have been applied to — . A, and to this extent at least the vector A is still arbitrary.

Direct substitution of (2.10) is terms of the potentials into (2.11) gives

(2.13) n curl curl A = J - e (grad ∂/∂t + ∂2A/∂2t ).

Using the vector identity

(2.14) curl curl A = grad div A - —2 A

we obtain

(2.15) grad n div A - n —2 A = J - e grad ∂f /∂t - e ?2A/∂t2

or

(2.16) grad( n div A + e ∂f /∂t) = n —2 A - e ∂2 A/∂t2 + J.

Since the vector potential A is still not completely defined, it is possible to assign any convenient value to div A. Let the definition of A be completed by a gauge condition commonly known as the Lorentz condition

(2.17) n div A + e ∂f /∂t = 0.

This reduces the above differential equation for the vector potential A to the simpler inhomogeneous wave equation

(2.18) n —2 A - e ∂2A/∂t2 = - J.

Another important gauge condition used in static and steady-state periodic problems is the Coulomb gauge specified by

(2.19) div A = 0

in which the potentials are determined by the differential equation

(2.20) n —2 A - e ∂2A/∂t2 + J = e grad ∂f/∂t.

Furthermore we shall assume that the volume charge density is equal to zero (in our conductor r vanishes) i.e.:

(2.21) div E = 0.

One approach in solving the skin effect problems is to separate the current density vector into two components

(2.22) J = Js + Je

where the source current density vector is given as follows:

(2.23) Js = - s grad f = - s ( df/dx e1 + df/dx e2 + df/dx e3 )

where e1 , e2 , and e3 are the unit vectors.

The eddy current density vector is given as

(2.24) Je = - s ∂A/∂t = - s ∂/∂t (e1 Ax + e2 Ay + e3 Az)

where Ax, Ay, and Az are the components of the vector A. However, it should be noted that neither Js nor Je can be measured physically, they are introduced only for mathematical convenience. Only the total current or the surface current density can be measured physically, and therefore only J or Ja (surface current density) provides a meaningful description of the current density distribution in the conductor. Let

(2.25) J = s E

and let

(2.26) E = - ∂A/∂t.

Now the differential equation (2.18) for the vector potential A can be written as

(2.27) n —2 A - s ∂A/∂t - e ∂2A/∂t2 = 0.

This equation differs from the previous equation in that the term ∂A/∂t appears together with the conductivity .

In a nonferromagnetic metallic conductor (made of copper) the above equation reduces to:

(2.28) n —2 A - s ∂A/∂t = 0.

In other words, the variation is such that the displacement current density ∂D/∂t is negligible compared with the conduction current density J in the conductor where the current flows. This is a standard engineering approximation for the problem with which we will be concerned and is used in

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 2.2 Cylindrical current carrying conductor with an elementary volume dt.

 

all the engineering texts cited in the references, e.g. Miller [2.3] Basically, we are stating that the events which we are studying happen at a much slower speed than that of the speed of an electromagnetic wave traveling through the media.

Equation (2.28) is the three dimensional diffusion equation which will be solved numerically by finite differences and by finite elements (but only in two dimensions). Moreover, it is evident that if the scalar and vector potentials are known, the electromagnetic vectors E and B may be calculated directly from (2.8) and (2.26).

In the case of separating the current density into two components Js and Je, we may combine equations (2.22), (2.24) and (2.18) to give

(2.29) n —2 A - s ∂A/∂t - e ∂2A/∂t2 = - Js

In equations (2.27) and (2.29), the second term on the left-hand-side is derived from the conduction current and the third term is derived from the displacement current. For a conducting metallic conductor, the displacement current is neglected in our application and we get:

(2.30) n —2 A - s ∂A/∂t = - Js.

In the last equation, the vector potential A and the source current density vector Js are unknown, (see figure 2.2).

 

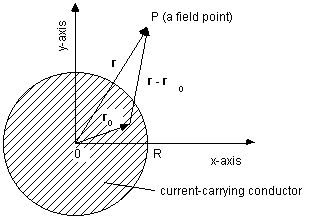
The Electrical Skin Effect in a Cylindrical Conductor

If a direct current flows through a long cylindrical conductor, it will be uniformly distributed over the cross-section of the conductor, hence the direct current density vector J is constant. With alternating or transient current, however, the current distribution is not uniform Angot [2.4] and tends to flow close to the surface of the conductor. The internal magnetic flux Fi, represented by the magnetic induction lines B(r) which circulate in coaxial circles about the axis, induces an opposing current in the central part of the conductor as the flux varies with time. The current density vector J(r, t) is thus reduced in the interior part of the conductor as compared with the current density near the surface. This phenomenon is known as the skin effect or the Kelvin effect and can be calculated with the aid of the magnetic vector potential. For the case that we will consider, the cylindrical symmetry implies

A = (0, 0, Az(r, t)), which satisfies the following differential equation [2.5]: (see figure 2.2)

We must also bear in mind that in this case the displacement current ∂D/∂t is neglegibly small and can therefore be neglected. We can write the left hand side of equation (2.31) as

(2.32) — ¥ ( — ¥ A ) = — ( — . A) - —2 A

The divergence of Maxwell's first equation yields

(2.33) — . ( — x H) = — . J

From vector identities, it is well known that div curl of a vector is always zero, and therefore Marsden and Tromba [2.6]

(2.34) — . ( — ¥ H) = — . J = 0

and substitution for

(2.35) J = - s —f - s ∂A/∂t

gives

(2.36) — . J = — . (-s ∂A/∂t) - — . (s —f) = 0

The divergence of the current density vector is always zero.

Since s is independent of spatial coordinates, equation (2.36) becomes

(2.37) - s ∂/∂t(— . A) - s —2 f = 0

or in cylindrical coordinates

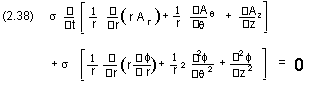
Equation (2.37) or (2.38) imposes a generalized divergence condition on A in terms of a scalar potential f. Equation (2.38) models the eddy currents in the conducting cylinder.

Furthermore in our special case of a conducting cylinder,

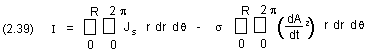
(see Fig. 2.3).

 

 

 

 

 

Fig. 2.3 Cross-sectional area of a conductor.

The peculiar form of equations (2.38) and (2.39) is probably the reason so many elaborate methods of solving eddy current problems have been developed.

Now the magnetic field intensity at the outer surface of the above conducting cylinder can be calculated from Ampere's law

(2.40) HR = I/2pR ; BR = m0 HR

where

I ... is the net current which flows through the cylinder and

R ... is the radius of the cylinder in meters.

3. Induced electric field from a time-dependent current.

In our problem, we ask what induced electric field exists in the vicinity of a long straight conductor carrying a time dependent current. ( See reference [2.7, 2.8, 2.9]. The similar problem of steadily increasing current in a cylindrical conductor was solved by Shakur [2.10] and commented on by Gauthier [2.9], Heald [2.7] and Chervenak [2.8]. However, a much more complete analysis including quantitative numerical results is needed. Shakur assumed that the skin effect is not important and that the electric field intensity is zero on the axis of the conductor. Furthermore, in his solution of uniformly distributed current desity over the cross section of a conductor, the electric field intensity is increasing with distance from the conductor. Fully defined electromagnetic problems are those in which all fields go to zero at large distances. In our analytical, finite difference and finite element solution to the practical problem, we will show that the current density in a cylindrical conductor will rapidly increase with radial distance from the conductor axis at 0.125 msec, 0.5 msec, 1 msec. At 0.005 msec, practically all current flows at the outer surface of the conductor

Moreover, we found that the current density is almost zero at the middle of the conductor (see Appendix B and Appendix C). We first introduce a return path for the current consisting of a coaxial cylinder at a radius r as indicated in figure 2.4. When r -> •, we have an isolated conductor.

 

 

 

 

 

 

 

Figure 2.4 Infinitely long conductor with a coaxial return.

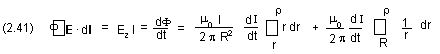
Therefore

for r≤R,

for R ≤ r ≤ r, and

(2.44) Ez = 0

for r > r.

We find that the electric field intensity has its maximum on the axis of the current carrying conductor and decreases with distance, r, from the conductor. Furthermore, it should be noted that E(r, t) is continous across the surface of the conductor.

 

 

 

 

 

 

 

 

 

 

Figure 2.5 Internal Fi and external Fe magnetic flux.

 

4. Magnetic Vector Potential.

The magnetic vector potential A and the magnetic flux in the conductor (see figure 2.5) and also in the surrounding medium (air) can be calculated with the aid of Stoke's theorem. The integration path follows the surface of the conductor parallel to the axis and returns at a distance r from the axis (see figure 2.6).

 

 

 

 

 

 

 

 

Figure 2.6 A long conductor of circular cross-section carrying a current I(t). A part of the conductor is removed to show the magnetic flux F and the path of integration for calculating the magnetic vector potential A on the inside.

Since the magnetic potential vector must be parallel to the current density vector J, and since for a long conductor, it is independent of the axial coordinate z, then,

where ez is the unit vector in the direction of the z-axis, A(r) is the magnitude of A at the radius r, and Fi is the flux through the radial plane surface enclosed by the path, see Laud [2.11]

However it should be noted that the right hand side of the above equation is only valid in the case of a steady-state problem. Hence this is the asympotic solution to the transient problem. If we assume that Az is zero at r=R, a comparison of equations (2.45) and (2.46) gives

(2.47) Az(r) = m0 I / 4 p (1 - r2/R2)

The external magnetic flux (for the region outside the conductor) is calculated similarly (this expression is independent of the current distribution) outside the conductor, see figure 2.5, see Hanka[2.12] and Shakur [2.10]. Integration of equation (2.43) with respect to time and applying Stoke's theorem gives the flux outside the conductor

(2.48) Az(r) = m0I / 2p ln(r/R)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Fig. 2.7 A view of the conductor in three dimensional space illustrating the geometry of the vectors.

Fig. 2.8 A cross-sectional view of a conductor illustrating the vectors r and r0.

The vector function A(r) can be found from a more general expression for the magnetic vector potential [2.13]

where t is the region representing the conductor, r is the position vector at which the value of the magnetic vector potential is desired, and r0 is the position vector to an elementary volume element dt, with the integration being carried out as r0 varies over all points of space in which J is not zero (see figure 2.7). From this formula it is easily seen that the vector potential A must be parallel to the current density vector J and hence to the z-axis of our coordinate system.

However, the vector potential for a long straight conductor carrying a transient current could not have been obtained from equation (2.49). The integral would diverge owing to the infinite extent of the conductor [2.14]. Integrating the previous equation with respect to z gives the magnetic vector potential once the current density distribution is known (see figure 2.8)

where F is the cross-sectional area and dF is the elementary area. At the interface between two media, the boundary constraints require continuity of the normal component of the magnetic flux density and the tangential component of the magnetic field intensity

where i and e denote the internal and external component of the vector, respectively.

5. Conclusion

The problem of electromagnetic field diffusion are in most cases classical boundary value problems solved for the magnetic and electric field intensity vector.

Modern solutions with important applications have gone though an evolution owing to the stress recently laid on the magnetic vector potential and transient operating conditions with the source current density term (see equations 2.27 and 2.29).

References

[2.1] Lorrain, P. and Corson, D. R., Electromagnetic Fields and Waves., W.H. Freeman and Company, New York, (1970).

[2.2] Ferraro, V. C. A., Electromagnetic Theory., University of London, The Athlone Press, (1954).

[2.3] Miller, K. W., " Diffusion of Electric Current into Rods, Tubes, and Flat Surfaces," AIEE Transactions (1947), 66, pp. 1496-1504.

[2.4] Angot, A., Compléments de Mathématiques a l'usage des ingenieurs de l'Electrotechnique et des Télécommunications, sixieme edition. Paris, Masson et Cie. (1972).

[2.5] Kalichman, S. A., Transient Electromagnetic processes in a Cylindrical Conductor During Impulse Magnetic Fields., Elektrichestvo, No. 9, pp. 60-63, 1981.

[2.6] Marsden, J. and Tromba, A., Vector Calculus, 2nd edition, W. H. Freeman and Co., San Francisco, 1981.

[2.7] Heald, M. A., "The Induced Electric Field from a Time-dependent Current," American Journal of Physics, 54 (12), December 1986, pp. 1142-1143

[2.8] Chervenak, J. G., The Back Electric Field from a Long Wire. American Journal of Physics, 54 (10), October 1986, pp. 946-947,

[2.9] Gauthier, N., "The Induced Electric Field Due to a Time-Dependent Current," American Journal of Physics, 53(6), June 1985, p. 519; 53(11), November 1985, p. 1037.

[2.10] Shakur, M. A., "The Induced Electric Field in a Long Straight Wire Carrying a Current that Increases in Time," American Journal of Physics, 52 (9), September 1984, P. 849. See also p. 785.

[2.11] Laud, B. B., Electromagnetics, Halsted Press, John Wiley and Sons, NY (1983)

[2.12] Hanka, L., Electromagnetic Field Theory, State Engineering Publishing House, Prague, (1975)

[2.13] Reitz, J.R. and Milford, F. J. and Christy, R. W., Foundations of Electromagnetic Theory. Addison-Wesley Publishing Co. Inc., Reading, Mass. (1980).

[2.14] Purcell, E. M., Electricity and Magnetism, 2nd ed, Vol. 2 McGraw-Hill Book Co., (1985)